Secondo il teorema di Umbeltodt, occorre la commistione di tre fattori affinché il tempo possa piegarsi in maniera esponenziale, lasciando trascorrere quattro ore nel periodo soggettivo di circa 16 o 17 minuti. Punto primo, un gruppo di amici sufficientemente affiatati e armati di trombette sudamericane. Punto secondo, qualcosa di accattivante da guardare in televisione, diciamo ad esempio, una finale di campionato. E punto terzo, cibo in grado di solleticare le papille gustative di tutti i presenti, in quantità sufficiente da raggiungere la sazietà. Che tipo gioviale, quel Wolfram Umbeltodt! Un’ottima forchetta e grande appassionato di pallone. Tuttavia devoto, al di sopra di ogni altra cosa, al suo dovere di professore…. E puntuale in ogni cosa che faceva. Ragioni a causa delle quali mai e poi poteva capitargli, durante una delle sue serate d’alterazione spaziotemporale, di crollare addormentato sul più bello della situazione, sperimentando quel momento in bilico tra il sogno e la veglia, dove la logica cessa di condizionare l’esperienza umana. Causando, certe volte, l’esperienza transitoria dell’ispirazione.
Quanti di voi conoscono, d’altra parte, la figura iper-entusiastica di Clifford Stoll? L’astronomo, autore e professore del Lawrence Berkeley Laboratory, che dopo aver fatto della matematica una ragione di vita, si è dedicato al collezionismo di antiche calcolatrici meccaniche, la produzione in serie di bottiglie di vetro e le profezie non sempre esatte sul futuro catastrofico del mondo digitale. Un personaggio associato indissolubilmente, almeno per il popolo di Internet, al canale scientifico di Numberphile, dove presenta ad intervalli regolari curiosità scientifiche strettamente interconnesse ai temi ai lui più cari. Tra cui: l’applicazione dell’ogiva gaussiana ai monotoni strumenti musicali da stadio, piuttosto che il piatto italiano probabilmente più famoso al mondo. È uno strano approccio alla questione, il qui presente, sopratutto per il fatto che, qualora decidiamo d’interpretarlo in modo letterale, sembra distruttivo degli assiomi stessi alla base della nostra relazione con l’Universo. Già, la cosiddetta “geometria euclidea”. Quel sistema così antico e duraturo, nonostante le evidenti limitazioni, che per quasi 24 secoli avremmo potuto chiamarla semplicemente “la geometria”. Che riduce tutto ad una serie di precise connessioni, riuscendo in questo modo a dominare le nozioni stesse dell’esistenza. Eppure siamo qui riuniti, oggi, per prendere nota di un’inaspettata situazione: quella in cui, grazie alle condizioni idonee, ogni previsione smette di condizionare alcunché. Lasciando il posto a un nuovo tipo di poligoni: magnifici quadrati con cinque lati.
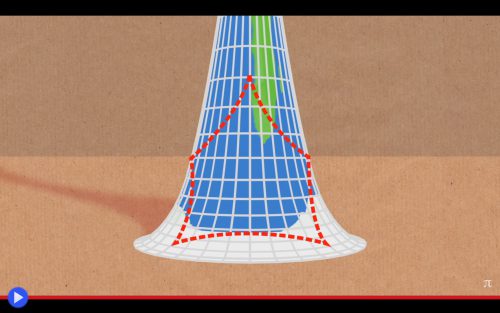
Riesco quasi ad udire le proteste dei tifosi sugli spalti, mentre l’apparente evidenza di quello che deve necessariamente essere un gioco di prestigio si presenta spontaneamente dinnanzi ai loro occhi, durante un concitato intermezzo di metà partita. Eppure, qualora si scelga di procedere per gradi, tutto sembra avere un senso. Prendiamo l’elemento di partenza, ovvero la fondamentale trombetta diventata celebre nel mondo durante i mondiali del 2014 tenuti in Brasile, per il suo suono terribilmente forte e monocorde. Ovviamente, voi non sentirete mai il buon Umbeltodt chiamarla Vuvuzela, bensì “Tromba dell’Arcangelo Gabriele”…. O per quanto concerne il professore americano dalla selvaggia chioma, beh, devo ammettere che non saprei dire. Ma sia chiaro che un simile nome, tanto altisonante e all’apparenza fuori luogo, è in realtà la reale definizione usata in geometria, per riferirsi all’esatta metà di una pseudosfera, che come aveva scoperto nel XVII secolo il matematico italiano Evangelista Torricelli (un nome, un programma) tende naturalmente all’infinito. Pur avendo un’area innegabilmente finita, tanto che si dice che la giusta quantità di vernice potrebbe ricoprire totalmente la sua superficie, a patto che possa essere “infinitamente diluita”. Paradossi a parte, è innegabile che esista una precisa caratteristica di un tale solido, se così scegliamo ancora di chiamarlo, particolarmente valida ad evidenziare l’effetto alla base dell’esperimento di Stoll: la sua capacità di essere convesso in ogni suo singolo punto. Modificando così profondamente l’interrelazione tra gli angoli e i segmenti, ovvero il concetto stesso della verità euclidea. Prima di addentrarci nel come tutto ciò possa accadere, direi che è giunto il momento di fare un piccolo snack…
topologia
Il taglio che recide l’illusione del panino imperfetto
L’onnipresente legge del karma che dirige ogni azione del nostro essere, verso la ricerca di un modo per esprimere noi stessi di fronte all’indifferenza dell’universo? Tra l’incolore moltitudine della gente? Senza una ragione ulteriore, né reali propositi di guadagno personale: se voi riceveste, oggi stesso, il dono temporaneo dell’assoluta onnipotenza, sono pronto a scommettere che una delle vostre prime decisioni suonerebbe più o meno così: “Genio della lampada, per piacere. Risolvi subito il problema della fame del mondo.” Il che inevitabilmente, potrebbe implicare vie risolutive chiaramente distinte. A seconda del TIPO di approccio scelto dallo strumento della vostra volontà immanente. Ciò che intendo è che c’è sempre una strada alta (bombastica, estrema) ed una che ti porta a camminare sul fondo ombroso della valle (il Dio invisibile ma onnipresente) verso il raggiungimento dello stesso obiettivo. Che dunque potrebbero corrispondere, in tale specifico caso, in: 1 – Moltiplicazione dei pani e dei pesci, trasformazione dell’acqua in vino 2 – Equa divisione dei pani, dei pesci e del vino. È in effetti sorprendente quanti tra coloro che perseguono il Paradiso, attraverso una serie di virtù che includono l’altruismo e la carità, siano inerentemente inconsapevoli di come sia del tutto possibile, oggi come ieri, ottenere una divisione equa delle risorse per l’organismo coloniale che noi definiamo Pianeta Terra. L’unica cosa che ci servirebbe per farlo, è il dono dello sguardo assoluto. La capacità di dividere ogni cosa a metà. Come dite, non sempre questo è possibile? Un mero luogo comune, questo. Come postulò, per primo, il matematico polacco Hugo Steinhaus.
Il teorema del panino al prosciutto è una di quelle dimostrazioni matematiche che sembrano contro intuitive, ovvero palesemente scollegate dalla verità dei fatti, laddove in effetti pervadono ogni singolo recesso del nostro metodo per rapportarci all’esistenza. Esso afferma che, presi tre oggetti in uno spazio tridimensionale, è sempre possibile suddividerli in due metà perfettamente equivalenti con un singolo iperpiano dimensionale. Il che indica, in termini più immediatamente comprensibili e chiari, il singolo taglio di una katana. Ci scherza un po’ sopra, la dottoressa Hannah Fry nel suo nuovo video per il canale di YouTube Numberphile, evidenziando assieme alla voce fuori campo come un alto numero delle cognizioni matematiche più rilevanti sembrino essere nate all’interno delle caffetterie universitarie, come se il momento del pranzo fosse in effetti quello più produttivo nella giornata di questa intera categoria di scienziati. Ma questo è, di nuovo, riconducibile alla dottrina e i metodi meditativi di alcune correnti interne al buddhismo Mahayana. Meditazione Zen: comprendere il senso, mentre la mente è vuota. Nessuna preoccupazione, niente pensieri sull’immediato. Soltanto due fette di pane, non importa quanto frastagliate, ed una di prosciutto magari anche ripiegata su se stessa (il formaggio? Non pervenuto, mi spiace). E un tagliente coltello. Adesso immaginate la scena: lo stimato professore, già celebre per i grandi contributi al campo dell’analisi funzionale, che gira da un lato all’altro del tavolo, spostando di volta in volta questo o quel componente primario del suo umile pasto, mentre ne toglie e fagocita un pezzettino dopo l’altro. Rendendolo irregolare e spostandolo, perché se analizzate le implicazioni di una simile affermazione, “sempre possibile” comprenderete che i tre pezzi non dovranno trovarsi esattamente uno al di sopra dell’altro. Potranno anche essere in due piatti diversi. Diamine, potrebbero essere stati posizionati in degli UNIVERSI a incalcolabili anni luce di distanza (certo per tagliarli, a quel punto, servirebbe la forma finale di Gurren Lagann).
Ora, sarà importante specificare come, in effetti, la linea di ragionamento, suggerita da Steinhaus, per la prima volta in un diario ritrovato a decadi di distanza presso l’Università dell’Illinois, poi dimostrata formalmente da Arthur H. Stone e John Tukey, non fornisca in alcun modo gli strumenti necessari a trovare la posizione esatta del taglio. Tutto quello che può fare per noi, è rassicurarci sulla sua mera esistenza. Ma come direbbe il più grande e famoso dei samurai, Miyamoto Musashi, non è forse questo abbastanza per iniziare ad allenarci a cercarla? Tutto quello che occorre, è l’assoluta e indubitabile convinzione. Non soltanto il sospetto, che potremmo riassumere in: posso posizionare la lama in modo che il panino sia per il 100% da un lato. E posso farlo affinché sia per il 100% dall’altro. Dal che deriva… No, c’è un modo molto più esaustivo e totalizzante, per comprendere istantaneamente il teorema…
Lo strano fascino dei toponimi spropositati
La strada di ciottoli verdi sembrava perdersi all’orizzonte, mostrando la vera distanza percorsa fino ad allora “Sei giunta assai lontano dal Galles, mia piccola Órfhlaith” disse lo spaventapasseri, mentre i due uscivano dall’alto palazzo del druido di Ohz. “Come pensi di tornare a casa?” L’uomo di latta camminava pensierosamente poco dietro al duo, finalmente cosciente dei sentimenti umani, mentre Bearnard l’orso, ansioso di mettere alla prova il ritrovato coraggio, si era già avviato per la sua strada, alla ricerca di un campo di battaglia al di la della grande Barriera. “Compagno di tante avventure, non devi preoccuparti. Sappi che la Morgen dell’Est, nel momento in cui è crollata sotto il peso del Dolmen della Collina Solitaria, grazie all’aiuto vostro e degli altri eroi, ha dimenticato di far seppellire anche i suoi piedi, ai quali si trovavano i mitici stivali di Víðarr. Ora indovina cosa nascondo nella mia sacca da viaggio?” Con un gran sferragliare, il loro amico si fermo di scatto, chiedendo d’istinto: “Un altro sacchetto d’uva spina?” Spaventapasseri si portò la mano sul volto, meditando sul fatto che dopo tutto, forse, non sarebbe stato l’unico ad aver avuto bisogno di un nuovo cervello. “Oh, oh, oh, mio guardiano dalla corazza istoriata. Sei sempre il solito. Ecco, amici, osservate!” Le calzature leggendarie rubate al popolo dei pirati di Mare, di un pacchiano color arancione, che si diceva potessero condurre gli eroi nel Valhalla. “…O dovunque essi vogliano, come mi è stato spiegato dal druido in persona. Per tornare al punto di partenza, dunque, non dovrò far altro che battere per tre volte gli speroni, mentre pronuncio, prima che l’eco si perda nel vento, il nome di casa mia.” Così detto, senza perdersi in chiacchiere inutili ed ulteriori, la principessa iniziò il rituale. Le nubi parvero convergere sulla loro posizione. Un corvo distante, gracchiando d’aspettativa, si alzò in volo per osservare. Órfhlaith fece una piroetta e diede il primo dei tre colpi THUMP: Llan-vire-pooll-guin… THUMP: …gill-go-ger-u-queern… THUMP …drob-ooll-llandus… Una pausa per riprendere fiato… ilio-gogo-goch… “Gogogoch?” Fecero eco i due testimoni, con gli occhi spalancati per lo stupore. Passarono uno, due, tre secondi. “Ha detto prima che l’eco…. Beh, credo che abbiamo un problema” Fece allora spaventapasseri, sforzandosi di soffocare una sghemba risata.
Se questa è una fiaba lievemente adattata alle circostanze, tuttavia, non significa che in essa manchi una significativa componente di verità. Per scoprire quale essa sia, basterà percorrere il vostro ponte preferito tra due, ovvero quello sospeso sopra lo stretto di Menai o il più moderno Britannia Bridge, per lasciare la terra dei Draghi gallesi sull’isola principale della Gran Bretagna, e transitare attraverso le nebbie della fredda isola di Anglesey. Scorgendo, chiaramente infisso nel terreno ai margini del sentiero asfaltato, quello che potrebbe essere uno dei più grandi cartelli stradali d’Europa. “Benvenuti presso la municipalità di “Llanvirepoollguin…” E via dicendo, per l’estensione di ben 58 lettere dell’alfabeto latino (benché considerata la lingua locale, esse vadano ridotte a “soli” 51 fonemi) Una roba da nulla, una vera quisquiglia da pronunciare *a patto di esservi nati o averci passato una parte significativa della propria gioventù, come l’attrice di Hollwood, Naomi Watts. Un luogo diventato particolarmente famoso quando, a settembre del 2015, il meteorologo della CNN Liam Dutton ebbe l’iniziativa, e la capacità, di pronunciarlo senza il benché minimo errore in diretta tv: Llanfairpwllgwyngyllgogerychwyrndrobwllllantysiliogogogoch, in tutto il suo strabiliante splendore, in grado di coprire da un estremo all’altro l’intera cartina proiettata alle sue spalle, tra lo stupore ed il reverenziale silenzio di ogni singola persona presente in studio. Ed a quel punto, era fatta. Tutti volevano saperne di più….
La realtà in merito all’insolita questione, in effetti, è che non siamo di fronte ad un nome particolarmente antico di qualche misteriosa lingua di tipo agglutinante, alla maniera in cui succede talvolta per i toponimi nord-americani risalenti all’epoca delle Nazioni Native (i quali, tra l’altro, non arrivano a una simile estrema profusione) bensì a una semplice trovata pubblicitaria, risalente alla metà del XIX secolo, quando la popolazione locale, su iniziativa di un sindaco che possiamo presumere particolarmente intraprendente, accettò l’insolita novità pur di comparire sulle mappe ed attrarre qualche turista di passaggio, aiutando l’economia. Prima di allora, in effetti, le cronache non sembrano riportare alcuno specifico nome per la comunità, fatta appartenere convenzionalmente all’antico feudo del marchese di Anglesey. Finché nell’ultima manciata di generazioni, forse anche in funzione della ritrovata celebrità, la popolazione non è aumentata in maniera esponenziale, raggiungendo la cifra attuale di di circa 3.000 persone. Tra le quali una percentuale di oltre il 70%, fatto particolarmente significativo, si dichiara ancora una parlante corrente della desueta lingua gaelica, che gli esperti ritengono prossima alla scomparsa dall’utilizzo attivo. E voi credete forse, che tutto questo sia un caso?
Il fabbricante di bottiglie con la quarta dimensione sotto il pavimento
La tipica villetta a schiera statunitense monofamiliare ha una forma estremamente riconoscibile, da fuori: il prato verde e ben tenuto, una grande finestra nel salone, un vialetto per raggiungere con l’auto il garage. La staccionata dipinta (si spera di bianco) e almeno un albero (di mele?) a ridosso della siepe che delimita lo spazio dei vicini. Più tre stanze da letto, due bagni e una grande cucina. Nient’altro potrebbe essere più ameno, ed anonimo di così. Ma nel contempo gli anni ed anni di racconti pseudo-fantastici, gialli, horror e d’altro tipo, ci hanno insegnato che l’assurdo più sfrenato tende a nascondersi proprio dietro a quelle mura in legno e intonaco, oltre cui la patina della normalità tende a dissolversi nel vento della soggettività, formando una particolare nebbia che corrode le rigide norme della razionalità. Può così succedere, facendo il nostro ingresso nella casa dell’astrofisico, ingegnere informatico ed hacker Clifford Stoll, di venire introdotti in un mondo totalmente inusuale. Affacciandosi da uno stretto pertugio, posto nel seminterrato di detta struttura, da cui è possibile accedere all’interfaccia tra l’edificio e il duro suolo. La lunga intercapedine che, se sufficientemente isolata dall’umidità, occasionalmente si trasforma in una sorta di cantina di riserva, sempre molto utile a chi nella vita di chi apprezza accumulare cose. Vi premetto, se non aveste ancora dato uno sguardo al video, che quest’uomo è una persona molto inusuali, così come tendono a esserlo le sue particolari collezioni (vedi ad esempio quella di calcolatrici meccaniche, su cui scrissi precedentemente). E quindi che dovremmo fare, a questo punto? Strisciare come vermi, o berretti verdi all’epoca della guerra del Vietnam, per entrare a testa bassa nel suo santuario sotterraneo? Niente affatto. C’è il robot semi-automatico con telecamera, per farlo. Un attrezzo auto-costruito per questa specifica ragione d’impiego.
Proprio così: progetti. La mente fervida s’impegna in molte cose. E un vero scienziato può essere, al tempo stesso, ricercatore, insegnante, ingegnere, o perché no! Risolvitore di problemi estremamente delicati. Ancor più famosa della dissertazione accademica sul moto dei pianeti scritta da Stoll, inclusiva di spunti piuttosto innovativi, fu infatti l’aiuto che diede nel 1986 al governo degli Stati Uniti, nella scoperta e cattura della spia russa Markus Hess, che aveva ottenuto illecitamente l’accesso illimitato ai server dell’università di Berkeley, oltre a quelli di altri 400 computer di varia importanza per gli Stati Uniti, con lo scopo di sottrarne le informazioni rilevanti prima di tornare in patria. Se non che fu proprio il nostro visionario amico, come contorno al suo lavoro, a tracciare alcune chiamate remote e permetterne la cattura, storia raccontata nel suo libro, mi dicono piuttosto romanzato, intitolato The Cuckoo’s Egg: Tracking a Spy Through the Maze of Computer Espionage. Trascorsa quindi l’era della gloria e delle sfide quotidiane, fra guerre di bottoni invece che fucili, ciò che resta fuori dal lavoro è solo tempo libero. Il che non significa, del resto, che sia necessariamente improduttivo.
Tutto ebbe origine, secondo il racconto enfaticamente esposto nel soprastante video, “qualche tempo fa” quando Stoll fu chiamato da un suo amico artigiano per aiutarlo a programmare il computer Macintosh da impiegare per il controllo remoto dell’ultimo modello di forno per la vetrofusione. Operazione al termine della quale, il professore scelse di essere pagato direttamente in natura: “Niente soldi.” Disse costui: “Costruiamo, invece, qualcosa”. I due presero quindi ad estrudere e plasmare il vetro, formando un bulbo tondeggiante con il collo stretto e lungo, simile a un cilindro. Quindi detta forma venne fatta curvare come un manico di teiera, e riportata a saldarsi con la superficie della bottiglia stessa. L’altra estremità di questa, nel contempo, è stata aperta sotto e ribaltata, andando a congiungersi con l’altro lato del cilindro. Avete capito di cosa sto parlando? No? Allora vi conviene continuare a leggere. Scoprirlo sarà per voi, ritengo, alquanto interessante.