Una visione che non può prescindere dalla latente percezione di un luogo diverso dalle aspettative, largamente collocato oltre i confini del catalogo di un mondo ed un contesto umani. Laddove non v’è nulla nella tipica pianura ricoperta di un accumulo di sodio, così elegantemente affiorato oltre la membrana della percezione, che esuli dal perfetto e prevedibile ordine della natura. Semplicemente essa non si configura, sotto alcuno degli aspetti ragionevolmente considerabili, come una comune contingenza sulla Terra, al punto che ben pochi tendono a comprenderne l’inusitata e inconfondibile bellezza. Né s’interrogano in modo frequente, per quanto possa risultare significativo, sull’aspetto complessivo di una tale situazione paesaggistica, ivi compresa la ripetizione modulare di uno schema che parrebbe la diretta risultanza di una sensibilità d’artista. La forma dell’esagono, nella cultura post-modernista, è del resto ricorrente come una diretta conseguenza della cosiddetta rule-of-cool, che attribuisce in modo per lo più intuitivo meriti esteriori ed un “carattere” a determinate contingenze matematiche, in maniera non dissimile da quanto fatto con le proporzioni del rapporto aureo nella scienza estetica del Rinascimento. Una visione del mondo, questa, che difficilmente può restare indifferente ad un paesaggio come quello dell’ormai prosciugato lago Owens, ricoperto da un reticolo di crepe tanto ricorsivo quanto sottilmente inquietante, nel suo ossessionante senso di ripetizione ininterrotta e misteriosamente precisa. Chi saprebbe ipotizzarne, dunque, l’origine? Chi, se non la dottoressa in scienze statistiche Jana Lasser del Max Planck Institute di Monaco di Baviera, che nel corso degli ultimi anni ha dedicato un susseguirsi di studi dedicati al fenomeno, ciascuno più specifico ed approfondito di quello precedente. Fino all’ultimo dello scorso 24 febbraio pubblicato sulla rivista Physical Review, all’interno del quale compaiono una serie di calcoli che parrebbero costituire l’effettiva prova, lungamente elaborata, della sua intrigante teoria. Poiché in molti si sono approcciati, attraverso l’incedere delle generazioni, alla saliente faccenda pur facendolo a suo avviso in maniera non risolutiva. Un’opinione che prevedo molti tenderanno a condividere, una volta preso atto delle basi solide del suo nuovo discorso. Lei ne cita, in modo particolare, due: Christiansen nel 1963, che individuava la causa di quel disegno nelle faglie generate dal gradiente di temperatura, a seguito di precipitazioni occasionali in luoghi di siffatta configurazione, come la Death Valley della California o la Salar de Uyuni in Bolivia. Così come Kinsley nel 1970, analizzando un luogo simile nell’entroterra iraniano, immaginava uno strato inelastico di suolo secco e perciò incline a distendersi, fino al punto di creare l’iconico susseguirsi di crepe poligonali. Entrambe cause possibili che nel nuovo studio, realizzato col supporto di una mezza dozzina di colleghi da diverse istituzioni austriache ed inglesi (la ricerca sul campo è stata niente meno che fondamentale) definisce come possibili ma cionondimeno soltanto “meccaniche”. Ovvero prive dell’ispirazione necessaria per raggiungere il fondamentale nocciolo della questione finale…
poligoni
Il quadrato al centro della pizza e la divina vuvuzela
Secondo il teorema di Umbeltodt, occorre la commistione di tre fattori affinché il tempo possa piegarsi in maniera esponenziale, lasciando trascorrere quattro ore nel periodo soggettivo di circa 16 o 17 minuti. Punto primo, un gruppo di amici sufficientemente affiatati e armati di trombette sudamericane. Punto secondo, qualcosa di accattivante da guardare in televisione, diciamo ad esempio, una finale di campionato. E punto terzo, cibo in grado di solleticare le papille gustative di tutti i presenti, in quantità sufficiente da raggiungere la sazietà. Che tipo gioviale, quel Wolfram Umbeltodt! Un’ottima forchetta e grande appassionato di pallone. Tuttavia devoto, al di sopra di ogni altra cosa, al suo dovere di professore…. E puntuale in ogni cosa che faceva. Ragioni a causa delle quali mai e poi poteva capitargli, durante una delle sue serate d’alterazione spaziotemporale, di crollare addormentato sul più bello della situazione, sperimentando quel momento in bilico tra il sogno e la veglia, dove la logica cessa di condizionare l’esperienza umana. Causando, certe volte, l’esperienza transitoria dell’ispirazione.
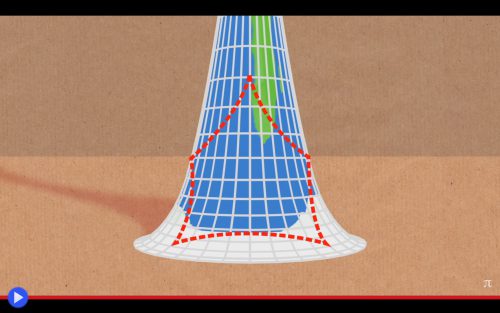
Quanti di voi conoscono, d’altra parte, la figura iper-entusiastica di Clifford Stoll? L’astronomo, autore e professore del Lawrence Berkeley Laboratory, che dopo aver fatto della matematica una ragione di vita, si è dedicato al collezionismo di antiche calcolatrici meccaniche, la produzione in serie di bottiglie di vetro e le profezie non sempre esatte sul futuro catastrofico del mondo digitale. Un personaggio associato indissolubilmente, almeno per il popolo di Internet, al canale scientifico di Numberphile, dove presenta ad intervalli regolari curiosità scientifiche strettamente interconnesse ai temi ai lui più cari. Tra cui: l’applicazione dell’ogiva gaussiana ai monotoni strumenti musicali da stadio, piuttosto che il piatto italiano probabilmente più famoso al mondo. È uno strano approccio alla questione, il qui presente, sopratutto per il fatto che, qualora decidiamo d’interpretarlo in modo letterale, sembra distruttivo degli assiomi stessi alla base della nostra relazione con l’Universo. Già, la cosiddetta “geometria euclidea”. Quel sistema così antico e duraturo, nonostante le evidenti limitazioni, che per quasi 24 secoli avremmo potuto chiamarla semplicemente “la geometria”. Che riduce tutto ad una serie di precise connessioni, riuscendo in questo modo a dominare le nozioni stesse dell’esistenza. Eppure siamo qui riuniti, oggi, per prendere nota di un’inaspettata situazione: quella in cui, grazie alle condizioni idonee, ogni previsione smette di condizionare alcunché. Lasciando il posto a un nuovo tipo di poligoni: magnifici quadrati con cinque lati.
Riesco quasi ad udire le proteste dei tifosi sugli spalti, mentre l’apparente evidenza di quello che deve necessariamente essere un gioco di prestigio si presenta spontaneamente dinnanzi ai loro occhi, durante un concitato intermezzo di metà partita. Eppure, qualora si scelga di procedere per gradi, tutto sembra avere un senso. Prendiamo l’elemento di partenza, ovvero la fondamentale trombetta diventata celebre nel mondo durante i mondiali del 2014 tenuti in Brasile, per il suo suono terribilmente forte e monocorde. Ovviamente, voi non sentirete mai il buon Umbeltodt chiamarla Vuvuzela, bensì “Tromba dell’Arcangelo Gabriele”…. O per quanto concerne il professore americano dalla selvaggia chioma, beh, devo ammettere che non saprei dire. Ma sia chiaro che un simile nome, tanto altisonante e all’apparenza fuori luogo, è in realtà la reale definizione usata in geometria, per riferirsi all’esatta metà di una pseudosfera, che come aveva scoperto nel XVII secolo il matematico italiano Evangelista Torricelli (un nome, un programma) tende naturalmente all’infinito. Pur avendo un’area innegabilmente finita, tanto che si dice che la giusta quantità di vernice potrebbe ricoprire totalmente la sua superficie, a patto che possa essere “infinitamente diluita”. Paradossi a parte, è innegabile che esista una precisa caratteristica di un tale solido, se così scegliamo ancora di chiamarlo, particolarmente valida ad evidenziare l’effetto alla base dell’esperimento di Stoll: la sua capacità di essere convesso in ogni suo singolo punto. Modificando così profondamente l’interrelazione tra gli angoli e i segmenti, ovvero il concetto stesso della verità euclidea. Prima di addentrarci nel come tutto ciò possa accadere, direi che è giunto il momento di fare un piccolo snack…