L’onnipresente legge del karma che dirige ogni azione del nostro essere, verso la ricerca di un modo per esprimere noi stessi di fronte all’indifferenza dell’universo? Tra l’incolore moltitudine della gente? Senza una ragione ulteriore, né reali propositi di guadagno personale: se voi riceveste, oggi stesso, il dono temporaneo dell’assoluta onnipotenza, sono pronto a scommettere che una delle vostre prime decisioni suonerebbe più o meno così: “Genio della lampada, per piacere. Risolvi subito il problema della fame del mondo.” Il che inevitabilmente, potrebbe implicare vie risolutive chiaramente distinte. A seconda del TIPO di approccio scelto dallo strumento della vostra volontà immanente. Ciò che intendo è che c’è sempre una strada alta (bombastica, estrema) ed una che ti porta a camminare sul fondo ombroso della valle (il Dio invisibile ma onnipresente) verso il raggiungimento dello stesso obiettivo. Che dunque potrebbero corrispondere, in tale specifico caso, in: 1 – Moltiplicazione dei pani e dei pesci, trasformazione dell’acqua in vino 2 – Equa divisione dei pani, dei pesci e del vino. È in effetti sorprendente quanti tra coloro che perseguono il Paradiso, attraverso una serie di virtù che includono l’altruismo e la carità, siano inerentemente inconsapevoli di come sia del tutto possibile, oggi come ieri, ottenere una divisione equa delle risorse per l’organismo coloniale che noi definiamo Pianeta Terra. L’unica cosa che ci servirebbe per farlo, è il dono dello sguardo assoluto. La capacità di dividere ogni cosa a metà. Come dite, non sempre questo è possibile? Un mero luogo comune, questo. Come postulò, per primo, il matematico polacco Hugo Steinhaus.
Il teorema del panino al prosciutto è una di quelle dimostrazioni matematiche che sembrano contro intuitive, ovvero palesemente scollegate dalla verità dei fatti, laddove in effetti pervadono ogni singolo recesso del nostro metodo per rapportarci all’esistenza. Esso afferma che, presi tre oggetti in uno spazio tridimensionale, è sempre possibile suddividerli in due metà perfettamente equivalenti con un singolo iperpiano dimensionale. Il che indica, in termini più immediatamente comprensibili e chiari, il singolo taglio di una katana. Ci scherza un po’ sopra, la dottoressa Hannah Fry nel suo nuovo video per il canale di YouTube Numberphile, evidenziando assieme alla voce fuori campo come un alto numero delle cognizioni matematiche più rilevanti sembrino essere nate all’interno delle caffetterie universitarie, come se il momento del pranzo fosse in effetti quello più produttivo nella giornata di questa intera categoria di scienziati. Ma questo è, di nuovo, riconducibile alla dottrina e i metodi meditativi di alcune correnti interne al buddhismo Mahayana. Meditazione Zen: comprendere il senso, mentre la mente è vuota. Nessuna preoccupazione, niente pensieri sull’immediato. Soltanto due fette di pane, non importa quanto frastagliate, ed una di prosciutto magari anche ripiegata su se stessa (il formaggio? Non pervenuto, mi spiace). E un tagliente coltello. Adesso immaginate la scena: lo stimato professore, già celebre per i grandi contributi al campo dell’analisi funzionale, che gira da un lato all’altro del tavolo, spostando di volta in volta questo o quel componente primario del suo umile pasto, mentre ne toglie e fagocita un pezzettino dopo l’altro. Rendendolo irregolare e spostandolo, perché se analizzate le implicazioni di una simile affermazione, “sempre possibile” comprenderete che i tre pezzi non dovranno trovarsi esattamente uno al di sopra dell’altro. Potranno anche essere in due piatti diversi. Diamine, potrebbero essere stati posizionati in degli UNIVERSI a incalcolabili anni luce di distanza (certo per tagliarli, a quel punto, servirebbe la forma finale di Gurren Lagann).
Ora, sarà importante specificare come, in effetti, la linea di ragionamento, suggerita da Steinhaus, per la prima volta in un diario ritrovato a decadi di distanza presso l’Università dell’Illinois, poi dimostrata formalmente da Arthur H. Stone e John Tukey, non fornisca in alcun modo gli strumenti necessari a trovare la posizione esatta del taglio. Tutto quello che può fare per noi, è rassicurarci sulla sua mera esistenza. Ma come direbbe il più grande e famoso dei samurai, Miyamoto Musashi, non è forse questo abbastanza per iniziare ad allenarci a cercarla? Tutto quello che occorre, è l’assoluta e indubitabile convinzione. Non soltanto il sospetto, che potremmo riassumere in: posso posizionare la lama in modo che il panino sia per il 100% da un lato. E posso farlo affinché sia per il 100% dall’altro. Dal che deriva… No, c’è un modo molto più esaustivo e totalizzante, per comprendere istantaneamente il teorema…
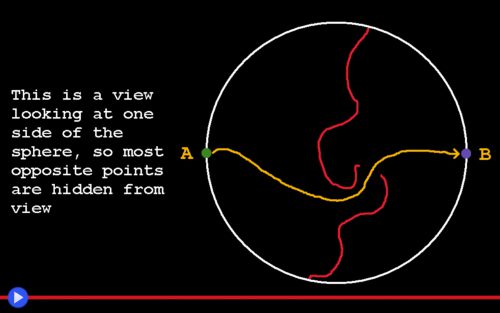
Nel diario in questione, intitolato il Libro Svedese, Steinhaus si poneva il problema dell’equa divisione del panino a partire da uno spunto d’analisi inaspettato: il teorema pre-esistente di Borsuk–Ulam. Il quale dimostrò a partire dal 1933, in maniera potenzialmente ancor più controintuitiva, che in ogni dato momento X, sulla Terra esistono un infinito numero di punti agli antipodi, in cui la temperatura, la pressione dell’aria o qualsivoglia altra metrica di misurazione atmosferica sono perfettamente identiche. “Ma come…” potremmo esclamare: “Se è vero che il sole può illuminare soltanto metà del globo, mentre qui è notte non può che conseguire che nel paese diametralmente opposto sia giorno.” E così via. Come può esserci la stessa temperatura? Tralasciando i calcoli matematici che come avrete ormai probabilmente compreso, non appartengono alla mia linea di ragionamento, ora pensate brevemente all’alternativa. Nel seguente modo: prendete una fetta dello sferoide su cui viviamo, definibile in geometria come il grande cerchio, ed appoggiatela sul piano cosmico della vostra immaginazione. Ora scegliete un punto a caso sul suo perimetro, chiamiamolo A, ed un secondo ai sui esatti antipodi, B. Mettiamoci due termometri. Ora ipotizziamo, solamente con finalità esplicative, che a si trovi alla temperatura di 20 gradi, mentre su B facciano -20. Ora saliamo su un aeroplano in grado di percorrere detta figura, ed iniziamo a trasportare il termometro A verso il punto B, mentre allo stesso tempo, un nostro aiutante sta facendo l’inverso col termometro B. Ora, poiché il primo dovrà vedere la sua temperatura scendere di 40 gradi Celsius, mentre al secondo accadrà l’opposto, ne deriva che entrambi passino, momentaneamente, per lo 0 spaccato. E se adesso vogliamo pensare che i rispettivi aeroplani si spostino alla stessa identica velocità, alla stessa altezza e senza alcuna interferenza da parte del sistema di pressurizzazione in cabina, ne deriva che tale momento sarà lo stesso per entrambi i termometri. Avete capito che cosa implica tutto questo? Essi si saranno al punto diametralmente opposto dello sferoide, l’uno rispetto all’altro. Se volessimo quindi ipotizzare, che tali punti “magici” fossero in quantità limitata, ne deriverebbe un ulteriore problema. Perché significherebbe che i due aeroplani potrebbero evitarli, scambiandosi di posto senza che la temperatura dei due termometri tocchi mai lo stesso identico valore. Il che vorrebbe dire, nei fatti, che continuerebbero entrambi a salire, oppure a scendere verso l’infinito. Congratulazioni: avete appena distrutto ogni forma di vita su questa Terra.
La dimostrazione del teorema di Borsuk–Ulam è fondamentale per risolvere la questione del panino al prosciutto, perché implica come una sfera possa essere proiettata su un piano bidimensionale, ottenendo delle precise corrispondenze tra i due punti di vista del “sopra” e del “sotto”. In altri termini, ogni cosa tridimensionale contiene se stessa due volte. Il che vuol dire che può essere divisa a metà. L’implicazione più interessante del postulato gastronomico di Steinhaus, del resto, è un’altra: esso può essere declinato per qualsiasi numero di dimensioni, reali o ipotetiche. Il che significa che possiamo prendere un ipotetico panino piatto, ed affermare che esso può essere diviso in parti uguali PURCHÈ non sia composto da più di due componenti (questo problema viene definito, generalmente, del doppio pancake). Ma anche che un panino dotato di un ulteriore strato, il formaggio, potrà essere diviso in parti uguali con un singolo iperpiano PURCHÈ la nostra mistica lama sia in grado di operare nella quarta dimensione. E così via per la quinta, la sesta, la “n”-esima…
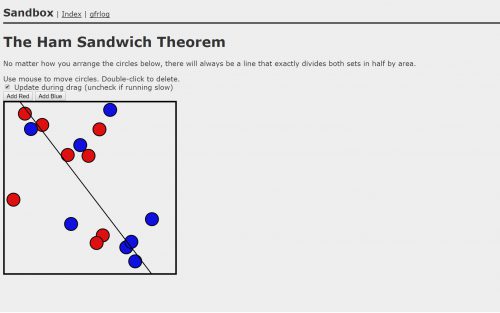
Dimostrare il teorema del sandwich in geometria discreta e computazionale è ancora più semplice. Si prende una certa quantità di pallini, rappresentanti rispettivamente delle “quantità” di pane e prosciutto, quindi si traccia una linea che ne mantenga il 50% da un lato, ed il 50% da un altro. Sembra un gioco della Settimana Enigmistica: è possibile trovare una posizione dei pallini che impedisca, a un samurai perfetto guidato dall’IA, di suddividerli equamente con un singolo segmento? Piuttosto che affermare ciò che sarà a questo punto ovvio, vi invito a fare da voi la prova sul sito soprastante, gentilmente fornito sulla pagina in html grigiastro di Gary Fredericks, dove lui “mette le cose” (come afferma in maniera impersonale ma formalmente corretta).
Potreste passarci anche svariati minuti (io l’ho fatto) soltanto per fallire ancora e ancora. Ma alla fine, comprenderete finalmente l’imprescindibile realtà: che la matematica è in ultima analisi soltanto un linguaggio, mirato ad interpretare l’effettivo funzionamento della realtà. E che non si può scegliere di rifiutarla, soltanto fare degli appunti sul metodo in cui viene espressa. Perché alla base di essa si trova la logica. Che è il fondamento stesso di ogni singolo prodotto del pensiero umano.


